Most találtam, de nem hagyhatom szó nélkül.

http://sirkan.iit.bme.hu/dokeos/courses/VIFO4319/work/49428093401b6bvh_raytrace.pdf

A GPU implementáció szempontjából a kd-fa jó választást jelent, miután az utóbbi években a
grafikus hardver számítási kapacitása elérte a hozzá szükséges szintet. A legújabb hardvereket
megel z en ugyanis problémát jelentett, hogy a fa bejárása rekurzív, ezért stacket igényel,
ami a GPU-n nem áll rendelkezésre.

page 14

Egy tévedés lapul meg a szövegben. Ezt írja:  a fa bejárása rekurzív, ezért stacket igényel,

Nos nem.

Hogyan lehetséges egy közönséges CG shaderrel rekurzíót írni? A kulcsszó: ugrási cím, mint textúra koordináta.

Generáljunk két textúrát, amiben majd egy pixelen tárolódik a fa ágait jelképező befoglaló doboz min és max értéke, vagyis a két sarka. Egy ilyen doboz ezzel a két vektorral egyértelműen meghatározható.

Járjuk be a CPU-n a fát a hagyományos módszerrel, közben tároljuk le a boxok min és max vektorait lineárisan, vagyis sorba a két textúrába.

A textúra koordinátát növeljük, miután letároltuk a vektorokat, de még mielőtt elágazna a fa. Hogy miért? Mert az elágazásból visszatérve még egy vektort le kell tárolni. Ez az ágat lezáró vektor egy harmadik textúrába kerül, de ugyan arra a textúra koordinátára, mint a doboz vektorai.  Ez a harmadik textúra pixel xy/red green/ komponense fogja azt a globális textúra koordinátát tárolni, amit az elágazásból visszatérve kapunk. Ez az adott ág vége a textúrában.

És ennyi a lényeg. Amikor fut a shader, akkor előveszi a befoglaló doboz két vektorát, meghatározza, hogy az adott ray metszi azt, vagy nem, majd ha nem metszi, akkor előveszi az ugrási textúra koodinátát a harmadik textúrából, és onnan folytatja a keresést.

Levágta az ágat, rekúrzíven működik a shader, mindenféle stack -nélkül, tehát ezt nem kell a rekúrzió eléréséhez.

Vannak még részletek, de a lényeg ennyi.

A harmadik textúra z /blue/ értéke tárolhatja azt, hogy egy levélhez ért az ág, és itt már háromszögekkel kell számolni. A háromszögek adatai néhány újabb textúrában tárolódnak, vertexek, az előre kiszámolt élnormálok és a tangens-vektorok a textúrázáshoz.

/  Érdemes újraolvasni, mert többször átírtam. Az első verzió több helyen érthetetlen. Lehet hogy ez is? /

Kis kitérő, bár a témánál maradok. A BVH fát a GPU-n is lehet generálni. Ennek az egyik módja a Morton-görbe, avagy Morton-code. A wikin átfutva elég rémísztőnek tűnik az egész, pedig ismét egy pofonegyszerű dologról van szó.

A BVH-tree felépítése úgy optimális, ha egy ág az egymáshoz közel eső primitíveket foglalja egybe. Nem is a távolságot szokás számolni, hanem a közös befoglaló doboz felületetét.

Egyenként lehet párba rendezni a primitíveket ezen értékek szerint, de ez sok ídő, ami realtime alkalmazásoknál és/vagy nagy polygon-szám esetén nem járható út. Megtehetjük azt, hogy a befoglaló leghosszabb éle irányát vesszük bázisiránynak, és a primitívek ezen koordinátái alapján rendezzünk. Aki már próbálta ezt a módszert, az tudja, hogy a keletkező fa messze nem lesz optimális. Az lenne az igazi, ha mindhárom tengely szerint tudnánk EGYSZERRE rendezni.

Nos, a Morton-görbével eszerint lehet rendezni. Egyszerre mindhárom térirány szerint.

Hogyan lehetséges ez? Egy végtelenül egyszerű módszerrel. A három koordinátából egyet készít. És nem bonyolítja túl a dolgot, simán összefésüli a három binárisan ábrázolt számot az  alábbiak szerint.

x(koordináta)  xbit3 xbit2 xbit1 xbit0 

y(koordináta) ybit3 ybit2 ybit1 ybit0

z(koordináta) zbit3 zbit2 zbit1 zbit0

Morton code          zbit3 ybit3 xbit3, zbit2 ybit2 xbit2, zbit1 ybit1 xbit1, zbit0 ybit0 xbit0

Itt most minden tér-koordináta egy négy bites szám. Úgy kell egybeolvasztani ezeket, hogy a keletkező szám akkor is közeli értéket adjon, ha a két eredeti koordináta x-ben volt közel, és akkor is ha y-ban, vagy z-ben. Ez úgy oldható meg, ha az alacsony bitek mind alacsonyan is maradnak, egymás után sorakoznak a Morton.code alján. A magasabb bitek 3 bitenként, csoportokban követik egymást.

Mint kitűnik, itt nem is igazán egy görbéről van szó, hanem egy speciális számábrázolásról, ahol összekeverjük a térkoordináták bitjeit. Mivel az egész ábrázoláshoz legtöbbször 32-bitet használnak, ezért egy koordinátára legfejebb 10 bit használható. Ez korlátozott felbontást jelen, a scene terének minden koordináta-tengelyét fel kell osztani 1024 részre. Ekkora az elérhető felbontás egy 32 bites Morton kóddal.

Ha eszerint a kód szerint rendezzük a primitíveket, akkor az egymáshoz közeliek egymás közelében maradnak rendezés után, így a fa közel optimásil lesz. Nem lesz olyan jó, mint a leglassabb módszerrel generált fa, de realtime fa generáláshoz sokkal hatékonyabb módszert ad a kezünkbe.

Sokan számolnak naponta mátrixokkal, de nem sokan ismerik mi is történik a mátrix rejtett fekete dobozában. Pedig könnyen megérthető, ha olyan mondja el, aki érti.

Legyen három koordináta-tengely, xv(1,0,0) yv(0,1,0) zv(0,0,1). Legyen egy pontunk a térben P(11,5,3). Bontsuk fel komponenseire, de ne csak úgy, kézzel, hanem felhasználva azt a megismert tulajdonságát a vektorok skalár szorzatának, hogy egy síktóli távolságot adnak meg, ha az egyik vektor egy sík normálja.

Felvesszük az origóból induló irányvektort, ami most ugyan az, mint a P.

w=P-O(0,0,0)=P

és komponenseire bontjuk.

P'.x=dot(xv,w)

P'.y=dot(yv,w)

P'.z=dot(zv,w)

Ez nem más, mint w vektor szorzása egy 3x3-as mátrixxal, amit 3 vektor alkot, az xv(1,0,0) yv(0,1,0) és a  zv(0,0,1).

A szorzás így néz ki.

P'.x=xv.x*w.x + xv.y*w.y + xv.z*w.z

P'.y=yv.x*w.x + yv.y*w.y + yv.z*w.z

P'.z=zv.x*w.x + zv.y*w.y + zv.z*w.z

Ez már egy teljes koordináta transzformáció.

Az elején a kivonást is beleolvaszthatjuk a mátrixba, ez volt a  P-O(0,0,0).

Ekkor a negyedik vektor az origó lesz. Az egész sokkal szebb, ha kiegészítjük 4x4-essé.

xv.x, xv.y ,xv.z , 0

yv.x, yv.y ,yv.z , 0

zv.x, zv.y ,zv.z , 0

O.x, O.y ,O.z , 1

Most transzformáljuk vissza a kapott P' vektort az eredeti állapotába. Ez úgy történik, hogy az origóból elindulunk xv irányba, és megteszünk P'.x távolságot. Nem nehéz kitalálni, miért. P'.x egy síktóli távolság, ennek a síknak  a normálja vx volt.

Ezután ugyan ezt tesszük yv és P'.y-al, majd zv és P'.z-vel. Egyenletekkel így néz ki ez az egész:

P=vx*P'.x + vy*P'.y + vz*P'.z

és kibontva:

P.x=xv.x*P'.x + yv.x*P'.y + zv.x*P'.z

P.y=xv.y*P'.x + yv.y*P'.y + zv.y*P'.z

P.z=xv.z*P'.x + yv.z*P'.y + zv.z*P'.z

xv.x, yv.x ,zv.x , 0

xv.y, yv.y ,zv.y , 0

xv.z, yv.z ,zv.z , 0

Mi a változás az előző mátrixhoz képest? A főáltóra türközve van a mátrix.

Ez az előző mátrix transzponáltja. A transzponált mátrixnak ez az értelme, fordított a hatása.

Első ránézésre nem nagy valami az egész, hiszen ugyan ez kézzel is elvégezhető. Igenám, de most forgassuk el az xv,yv,zv koordináta-rendszert. Meglepetésre most is jól működik az egész, annak ellenére, hogy mostmár kézzel szinte lehetetlen komponenseire bontani a vektort.

A BRDF modelek pedig csak gyenge közelítések, így lényegtelen mind. Hiszen a valóságban mi történik?

Van egy egyenetlen felület, ahonnan a fényhullámok a szuperpozició elvének megfelelően mindenfele verődve kialakítanak egy valószínűségi teret. Ez a komplex tér határozza meg, hogy hol, milyen és mennyi foton fogunk detektálni.

Egy helyes raytace vagy fotonmap hullámokkal számol. Ezt a jelenlegi számítási teljesítnény mellett lehetetlen megvalósítani. Egyetlen foton számítása is nagyságrendekkel több számítást igényel, mint egy ray vektor számítása.

A jelenlegi legjobb eredményt a monte carlo ray tracing adja. Nem véletlenül. Ez áll legközelebb a valósághoz.

Ennyi segítség elég ahhoz, hogy akár nulláról el lehessen kezdeni sugárkövetéssel foglalkozni.

Talán még a textúrázásról néhány gondolat, mert nem sok leírás tér ki a részletekre.

A normál polygon alapú grafikánál a háromszög három csúcsához tartozik 3 textúra koordináta. Ezek a texúra mappolását adják meg az adott háromszögre. Hogyan lehet ezeket raytrace-nél használni?

Minden felülethez rendelhető egy tangens-tér. Ha a tangens vektor a mappolás irányába áll, akkor ez felhasználható a textúrázáshoz. Erre is találunk leírást, ilyen mátrixok egyszerűen létrehozhatóak.

De mi miért van? Erről sehol nem lehet olvasni. Az egyenleteket kész tényként vágják hozzánk.

A mappoláshoz két vektor kell majd, ezek az u és v textúra koordináták tengelyeinek irányát mutatják majd a 3 dimenziós térben. A textúrák értelemszerűen 2 dimenziósak, u és v koordináták jelölik az x és az y tengelyeket, megegyezés és hagyomány alapján. UV mappolásnak is nevezik az adott technikát.

Az U és V vektorok 3 dimenzióban, azaz modeltérben a mappolási irányban állnak. De nem feltétlenül kell arra állniuk. Az itt részletezett megoldásban kissé egyszerűbb minden, így könyebb majd a lényeget megérteni.

Legyen egy háromszög v1,v2,v3 vertex koordinátákkal és uv1,uv2,uv3 textúra koordinátákkal. Más bemenő érték nem is kell.

Ezekből néhány alapvektor veszek fel.

nx=v2-v1

ny=v3-v1

nnx=normalize(nx)

uvx=uv2-uv1

uvy=uv3-uv1

nuvx=normalize(uvx)

Ezek a külső /model/ és belső /textúra/ koordináta-rendszerbeli vektorok, két élre felvéve. v1 csúcsból indul mind, az egyik v2-be megy, a másik v3-ba mutat. A normalizált vektorok irányvektorok és merőlegesség biztosítása lesz a feladatuk.

Az ny-nak merőlegesnek kell majd lennie az nx-re, és az uvy-nak az uvx-re.

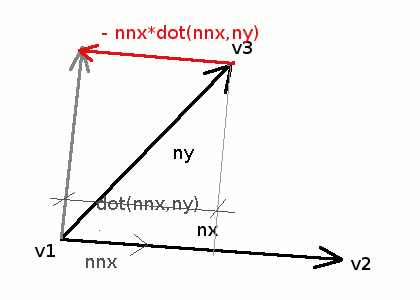
Ez egyszerűen elérhető. Az ny vektort az nnx-el beszorozva megkapjuk azt a komponensét, amennyi 'belelóg' az nnx irányba. Ez egyszerűen csak ki kell vonni az ny-ból, aminek eredményeként az merőleges lesz az nx-re. A kivonás 'iránya' nnx.

ny'=ny - nnx*dot(nnx,ny)

Ugyan ezt eljátszuk az uv vektorokkal is.

uvy'=uvy - nuvx*dot(nuvx,uvy)

Ezzel meg is kaptuk a belső koordináták számolásához megkívánt vektor-halmazt. ny merőleges nx-re, így lehet velük koordináta-transzformációt végezni.

De ehhez előbb el kell osztani őket a hosszuk négyzetével.

nx=nx/dot(nx,nx)

ny'=ny'/dot(ny',ny')

Ez ugyan az, mintha azt írnám hogy  nx=normalize(nx)/length(nx) , hiszen a normalizás is a hosszával osztja a vektort.

Ezzel elértem azt, hogy beszorozva egy vektorral, a kapott vektor hossza akkor lesz pontosan 1, ha megegyezik az eredeti él hosszával, például a v2-v1 vektorral. Nyilván ha v2-v1 10 egység hosszú volt, akkor 0.1-el kell szorozni, hogy egyet kapjak. Ezért osztottam a vektort 10*10-el.

Miért jó nekem ez az 1? Mert most rászorozva az első él textúra vektorát /uvx/, pontosan megkapom az uv2 mappolási értéket, ha hozzáadom még az uv1-et. Hiszen vektor*1=vektor.

w=metszéspont-v1

UVmetszéspont=uv1 + uvx*dot(nx,w) + uvy'*dot(ny',w)

Ez már így mappol, de túl sok vektort kellene letárolni /5-öt./ De átrendezhető az egyenlet, így elég 3 vektor, ami egy 3x3-as mátrixot ad.

kx=nx*uvx.x + ny'*uvy'.x

ky=nx*uvx.y + ny'*uvy'.y

így már sokkal egyszerűbb számolni

UV.x=uv1.x + dot(kx,w)

UV.y=uv1.y + dot(ky,w)

 Ez valójában egy vektor szorzása mátrixxal, ami megadja a metszéspont textúra koordinátáit.

Látszik, hogy a mappolás iránya se nem nx, se nem ny'.  nx az első él iránya, ny' erre merőleges.

De mégis helyes érteket ad az egyenlet. 

Ilyenformán el is értem az ismeretlen blogszerző által közölt mondandó végét. De van még tovább, nem is kevés.

Hogyan lehet egyszerűen meghatározni, hogy a felületi metszéspont egy adott háromszögen belül van vagy nem?

A neten szétnézve többé kevésbé szokványos megoldások leledzenek. Ezek kissé csúnyák, alulmagyarázottak, és legtöbbnél sokat kell számolni futásidőben. Itt egy olyan módszert mutatok be, ahol futásidőben csak három dot() kell.

Ha valaki nem olvas tovább, hanem az eddig leírtak alapján elképzel egy háromszöget, némi gondolkodás után akár meg is találhatja a most közetkező megoldást, hiszen egyszerű. A dot() távolságot ad egy síktól. Igen ám, de már a metszéspont rajta van az egyetlen ismert síkon.

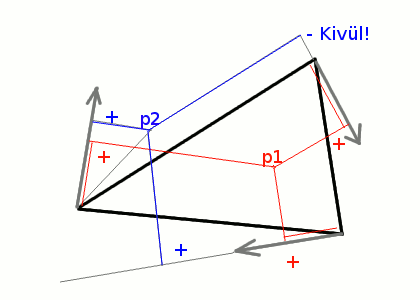
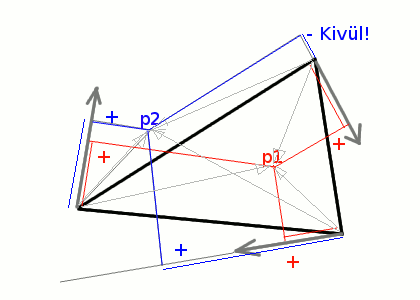
Akkor készítsünk még síkokat. Már nem nehéz kitalálni, három síkot kell még létrehozni. Ez a három sík közrefogja a háromszöget az éleinél . Mindegyik merőleges az alap síkra, és a háromszög egyik éle rajta fekszik az új síkon is.

Innen már mindenki magától is összeheggesztheti az egyenleteket, ha nem olvas tovább.

Ime a megoldás.

Egy olyan normált keresek, ami merőleges az adott sík normáljára és a háromszög egyik élére. Ez a probléma a cross() vektoriális szorzattal oldható meg. Ennek két bemenő paramétere van, és a kimenő vektor merőleges mindkét bemenő vektorra.

Ennek a jelőlése már az előző blogban látható volt, az n=(r2-r1) X (r3-r1) egyenletnél. Ez az X. A működése megérthető, ha behelyettesítjük az x(1,0,0) és az y(0,1,0) vektorokat az egyenletekbe.

Miután megkaptam az élnormált, meg kell vizsgálni, hogy a háromszög harmadik csúcsa fele mutat-e. Ha nem, meg kell fordítani, így mindig a pozitív tér lesz a helyes irány. Ugyanis a dot() szorzat egy pozitív és egy negatív térfélre osztja a teret ugyan úgy, mint a koordináta-tengelyek.

Miután megvan mindhárom élnormál, már lehet is használni őket. Vigyázni kell, hogy a vizsgálni kívánt pontba a vektort mindig abból a csúcsból húzzuk, ami rajta fekszik az élen. Ha mindhárom dot() pozitív számot ad, a vizsgált pont biztosan benne van a háromszögben.

t = (n*r0+ D)/ (nv)

Na ez igazán teljesen értelmetlen egyenlet. Vagy nem?

Kicsit módosítom, mert én ebben a formában szoktam meg.

t = (n*(r0-D))/ (nv)

Most ismét legyen a normál n(0,0,1). Ekkor ennyi marad :

t= (r0.z - D.z)/v.z

Ilyen formában talán bele lehet verni valami jelentést is. Ha D(0,0,0) akkor ezt is elfelejthetjük

t= r0.z /v.z

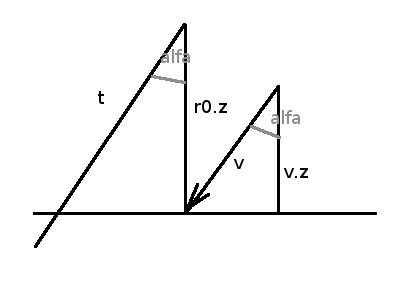Mi ez? Ez egy rejtett szögfüggvény. cos alfa=v.z/abs(v)=r0.z/t

t=r0.z*abs(v)/v.z

Mivel v egységvektor, amiatt abs(v)=1 vagyis t=r0.z /v.z.

Magyarul r0.z magasságból v irányban a síkot t távolságnál találjuk el.

Látható, hogy itt csak magasságokkal számoltam.  Az eredeti egyenletben ezért vannak a vektorok beszorozva a normállal, mert azok IS magasságokat adnak, csak relatíve a síktóli magasságot.  Ez már egy egyszerű koordináta-transzformáció volt, legalább is egy komponensre. Erről majd még írok.

 /kis kiegészítés: mivel v vektor z komponense negatív,  így a gyakorlatban az egyenlet ilyen: t= (D.z - r0.z )/v.z    illetve t = (n*(D-r0))/ (nv)   /

Rátaláltam egy láthatóan félbehagyott raytrace leíró blogra. Mivel nincs hasonló blog a közelben, gondoltam, az illető helyett befejezem.

http://despina.blog.hu/2010/12/15/metszespontszamitas_1

Az utolsó írásánál a metszéspont számítását vázolta fel. Ezt inkább csak vázlatnak tekinthető, hiszen az egyenletek szinte csak fel lettek írva. Hogy mi miért van úgy ahogy, az nem derült ki az írásból. Sőt a végén maradt egy elvarratlan szál is.

Akkor bele a közepébe.

Ott akadt el a magyarázat, hogy sík és egy egyenes metszete. Az egyenes egyenlete adott, és a t is kiszámolható, de miért így kell számolni ezeket?

r=r0 + t*v

Először lássuk az egyenest. Ennek van egy iránya, amit egy irányvektor ír le. Ez a v vektor. Ennek a hossza egy, magyarul normalizált vagyis egységvektor. Ilyen vektorokkal szokás az irányokat megadni. Az r0 az egyenes kiinduló pontja. Mivel t egy távolság, és ez általában pozitív értékű, emiatt az r az egyenes végpontja. A köztük levő távolság a t.

A vektoros alak könnyebben megérthető, ha először 1 dimenzióban nézzük az adott helyzetet.

Ha minden csak egy skalár, akkor r0 egy közönséges szám, amihez t*1 értéket hozzáadva r értéket kapunk. Igy nem is tünik olyan rejtélyesnek az egész. A vektoroknál 'csak' annyi történik, hogy 3 db ilyen skalárral dolgozunk és a v vektor egyik komponense sem 1, hanem az sqrt(v.x*v.x + v.y*v.y + v.z*v.z ) érték. Ez a v vektor hossza.

Bármilyen hosszúságú vektorból lehet egységvektort készíteni, csak el kell osztani minden komponensét a hosszával. Ez 1 dimenzióban magától értedődik. 1=x/x, mivel ott a vektor hossza maga az x. Ezt hívják a vektor normalizálásának. Shader nyelven ez a normalize().

Az egyenesek rejtélye után jöhet a következő állomás. Miért kell a sík-egyenes metszetét ilyen nyakatekerten számolni?

Először vegyük a sík egyenletét n(r-D) =0. Mit jelent ez?

Csak annyit hogy a felület minden pontja a síktól  zéró távolságra van. Ha bármilyen r térbeli pontba húzok egy vektort a felületet levő D pontból, akkor a kapott vektor és a sík normáljának a szorzata mindig nullát ad, ha az r pont a síkon van. Miért?

Ismét az egyszerűbb eset felöl kell a problémát megközelíteni. Legyen a sík az  xy sík, ennek a normálja a z tengely. D legyen a (0,0,0) . Nyilván a sík minden pontjának a z koordinátája zéró. Mivel a normál n=(0,0,1), igy vármilyen r-D vektor szorzata a normállal zérót ad.

Két vektor skalár szorzata ugyan olyan, mint amit a távolság definiciójánál már láttunk.

dot(v1,v2) = v1.x*v2.x + v1.y*v2.y + v1.z*v2.z

Ha r(5,3,0) és n(0,0,1) akkor dot(r-D,n)= 5*0 + 3*0 + 0*1 =0, csak az r.z komponens számít, a többi biztosan nullát adna.

Ez annyit jelent, hogy az r pont távolsága a D és n által megadott síktól nulla, vagyis a pont a síkon van. A vektorokban az a nagyszerű, hogy bármerre állhat a térben a normál, ugyan így működik. A vektorok skalár szorzata /dot()/ mindig egy távolságot ad, ha az egyik vektor normált.

Vannak még érdekes tulajdonságai ennek a szorzásnak. Az második ismerős, hiszen már leírtam, amikor távolságot számoltam. Ha egy nem egységhosszú vektort önmagával szorzunk, akkor a vektor hosszának négyzetét kapjuk. Ezért kell a gyökvonás a távolság számolásakor. Ezt szinte mindenki számolta már, csak nem tudta, hogy vektorok skalár szorzatát veszi.

A harmadik tulajdonsága is hasznos lehet, ez az az eset, amikor mindkét vektor normalizált. Ekkor a két vektor közötti szög cos()-át kapjuk eredményül. Ez sok mindenre jó, például egyszerűen világíthatjuk be a felületet mindenféle szögfüggvény nélkül.

http://en.wikipedia.org/wiki/Lambert's_cosine_law