Ilyenformán el is értem az ismeretlen blogszerző által közölt mondandó végét. De van még tovább, nem is kevés.
Hogyan lehet egyszerűen meghatározni, hogy a felületi metszéspont egy adott háromszögen belül van vagy nem?
A neten szétnézve többé kevésbé szokványos megoldások leledzenek. Ezek kissé csúnyák, alulmagyarázottak, és legtöbbnél sokat kell számolni futásidőben. Itt egy olyan módszert mutatok be, ahol futásidőben csak három dot() kell.
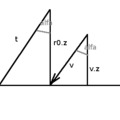
Ha valaki nem olvas tovább, hanem az eddig leírtak alapján elképzel egy háromszöget, némi gondolkodás után akár meg is találhatja a most közetkező megoldást, hiszen egyszerű. A dot() távolságot ad egy síktól. Igen ám, de már a metszéspont rajta van az egyetlen ismert síkon.
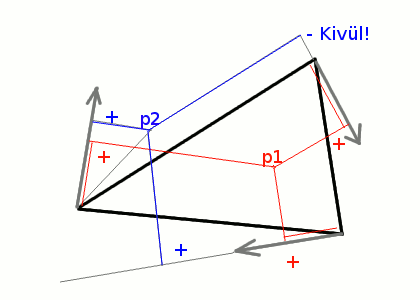
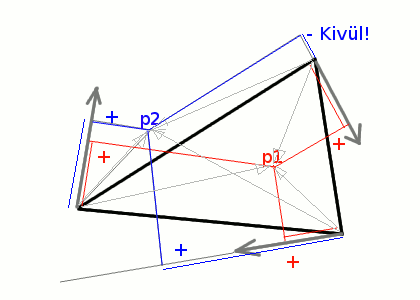
Akkor készítsünk még síkokat. Már nem nehéz kitalálni, három síkot kell még létrehozni. Ez a három sík közrefogja a háromszöget az éleinél . Mindegyik merőleges az alap síkra, és a háromszög egyik éle rajta fekszik az új síkon is.
Innen már mindenki magától is összeheggesztheti az egyenleteket, ha nem olvas tovább.
Ime a megoldás.
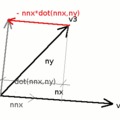
Egy olyan normált keresek, ami merőleges az adott sík normáljára és a háromszög egyik élére. Ez a probléma a cross() vektoriális szorzattal oldható meg. Ennek két bemenő paramétere van, és a kimenő vektor merőleges mindkét bemenő vektorra.
Ennek a jelőlése már az előző blogban látható volt, az n=(r2-r1) X (r3-r1) egyenletnél. Ez az X. A működése megérthető, ha behelyettesítjük az x(1,0,0) és az y(0,1,0) vektorokat az egyenletekbe.
Miután megkaptam az élnormált, meg kell vizsgálni, hogy a háromszög harmadik csúcsa fele mutat-e. Ha nem, meg kell fordítani, így mindig a pozitív tér lesz a helyes irány. Ugyanis a dot() szorzat egy pozitív és egy negatív térfélre osztja a teret ugyan úgy, mint a koordináta-tengelyek.
Miután megvan mindhárom élnormál, már lehet is használni őket. Vigyázni kell, hogy a vizsgálni kívánt pontba a vektort mindig abból a csúcsból húzzuk, ami rajta fekszik az élen. Ha mindhárom dot() pozitív számot ad, a vizsgált pont biztosan benne van a háromszögben.